
定量評価は人間の行動や感情を数値として読み解き、分析するのに欠かせない評価です。
私もウェブ解析や広告配信を行っていく中で定性評価を用いてレポートを書く機会が数多くあるのですが、その中でよく「平均値」を用いることがあります。
多くのデータの違いを均(なら)すことで算出される平均値は膨大なデータ一つ一つを見る必要がなくなり、「凡そこのような数値なんだな」と一見してわかるようになる素晴らしい値です。クライアントさまからも「結局平均はいくらなの?」とお尋ねされる機会も多くあり、レポートの中でも非常に大きな存在感を出す値であることは間違いありません。
しかし、統計を学んでいる人からすると平均値だけでデータを判断することは非常に危うい行為です。
今回は、そんな平均値の危うさとそれを解決するために何を見れば良いのかをご説明させていただきます。
そもそも“平均値”って?
そもそも平均とは「不揃いのないこと・ならすこと」という意味で用いられる単語であり、平均値とは「不揃いのないように均された値」という事です。
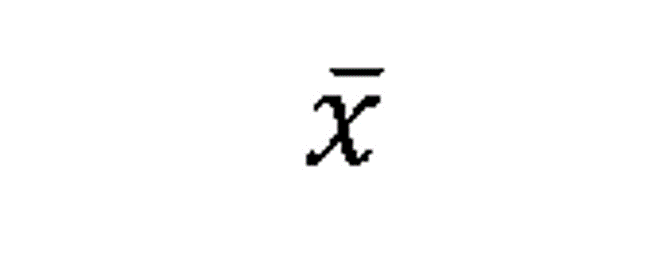
平均値はこのようにxの上にハイフンを載せた値で表されますが、今回の記事では便宜上xと表記させていただきます。
平均値-xは下記のような式で表記されることが多く、データ内の数値の和をデータの個数であるnで割った商として求められます。
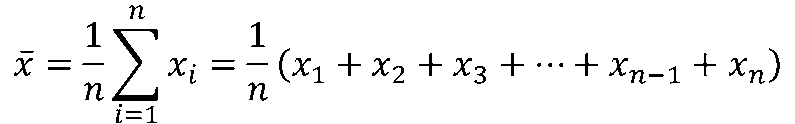
平均値を扱うメリットとしては、データ内のすべての数値の和を用いて算出される値なのですべての数値を考慮した値といて用いることが出来ます。
デメリットは“外れ値(他の数値から見て極端にズレた値。非常に大きい・小さいなど)”の影響をかなり強く受けてしまう、という事です。
例として、2つのサンプルデータを見てみましょう。


こちらのsampleA/sampleBは互いに平均値¯xは20です。sampleAは全ての数値x_iは20なので平均値が20だと言われても納得が出来ます。しかし、sampleBにおいて7番目の数値であるx_7以外は全て15以下であり、x_7が平均値を押し上げていることが伺えます。(この表においてはx_7は外れ値と呼ばれます)
外れ値は基本的に実験等における主に測定ミスや記録ミスから生じます。とは言っても明らかに測定・記録ミスの場合を除いてはデータ上から削除してはなりません。(意味のある外れ値の場合もありますし、データそもそもの信ぴょう性にも欠けてしまいます)
このような場合に使う値が「中央値」と「最頻値」です。
中央値(median)
中央値とはデータを小さい順に並び変えた時に中央に出てくる数値の事です。(データが偶数個ある場合ではその平均値が中央値となります)
sampleBの場合では中央値は11.5となります。

中央値は外れ値の影響をほとんど受けないというメリットがあります。
しかし、中央値はそのデータ単品で見るには良いのですが、平均値のように全体のデータから出される数値ではない為、データの推移などを見るには不向きな一面があります。
最頻値(mode)
最頻値とはデータの中において最も出現頻度の高い値の事です。
sampleBの場合では、2回出てきている15が最頻値となります。

データの個数のみで判断しますので、外れ値の影響を最も受けにくい値です。しかし値の出現頻度から見る性質上、データの個数が少ないと全体的に差が生まれず役に立たないことがあります。(なのでsampleBはあまり役に立ちません…)
代表値はどのように使い分ける?
さて3種類の値(代表値)について説明させていただきました。それぞれ特徴がありますが、どういった時に使い分ければいいのでしょうか。
使い分けの大きな目安としても用いられるのが「正規分布(ガウス分布)」です。
正規分布とは下図のように頂点のx座標が平均値¯xな、左右対称な曲線(釣鐘型)で描かれる分布です。
正規分布には下記のようなルールが存在しております。
σは標準偏差と呼ばれ、ExcelではCONFIDENCE関数で求めることが可能です。
この標準偏差σを考慮した範囲にデータがしっかりと存在する場合は、データが正規分布として分布しているので平均値を使うことが適しています。。しかし、この範囲にデータが存在しない場合はデータが散らばっている為(「分散している」という)平均値では無く、中央値などの値を使った方が良いとされます。
まとめ
平均値はあくまで不揃いなデータを均したものであり、実際の傾向や真ん中を示した値ではないという事が伝わったかと思います。
様々なデータを用いる中で平均値を使う場合もありますが、本当にそのデータでは平均値で表すべきなのか一度考える参考にしていただき、またレポートを受け取る方も平均値だけを見るのではなく実際のデータも参照するきっかけになればと思います。
ライター:うまのお肉





